for PSAT 자료해석: 가중평균 이론과 활용

PSAT 자료해석에 수학이 필요없다는 글을 썼지만, 그렇다고 수학을 전혀 모르는 사람이 필요한 스킬을 아는 사람과 똑같은 퍼포먼스를 낼 수는 없는 법이다. 꼭 알아야 하는 '기본기'에 해당하는 이론들이 당연히 있다(의무교육과정만 충실히 따라왔어도 알 수 있는 것들―아마도). 그 이론을 아는 것보다도 이론을 어떻게 활용하느냐가 더 중요하다. 그래서 쓰는 첫 글이다.

 

여러 개념들 가운데 가중평균만큼 많은 질문을 받았던 게 없어서 가중평균을 첫 글 소재로 삼기로 했다.

 

<다른 'for PSAT 자료해석' 글>

for PSAT 자료해석: 변화율(증가율)·비중 역산

가중평균을 위한 암산 훈련

가중평균이란?

초등학교 6학년 때 담임 선생님이 이런 질문을 했었다.

우리 반 남자애들 평균 점수가 30점이고, 여자애들 평균 점수가 36점이야. 그럼 우리 반 전체 평균 점수는 얼마지?

 

당시 나는 아주 자신있게 33점이라고 답했고 당연히 틀렸다. 그게 나와 가중평균의 첫 만남이었다.

 

엄밀히 말하면 선생님이 가중평균을 가르쳐주려고 한 건 아니었고, 산술평균의 함정을 보여주기 위한 질문이었다(저거 던져놓고 가중평균 하는 법은 안 가르쳐줬어!). 우리 반에는 여학생이 더 많았으므로 우리 반 전체 평균 점수도 36점 쪽으로 기울어진다.

 

우리가 태어나서 가장 처음 배운 '평균'은 정확히는 '산술평균'이라고 부르는 것이다. 관찰값의 합을 관찰값 개수로 나눠 구한다. 예를 들어, 국어 80점 수학 70점 영어 90점을 받은 학생의 평균 시험점수는 다음과 같이 계산된다.

 

그럼 가중평균은 뭐가 다른가? 가중평균에는 '가중치'가 개입된다. 각 관찰값마다 가중치를 설정해 관찰값×가중치를 가중치의 합으로 나눠 구한다. 이때 가중치의 합은 기본적으로 1이므로 사실상 관찰값×가중치의 합이 곧 가중평균이 된다(물론 가중치의 합이 1이 안되는 상황이 생길 수 있는데, 그때는 당연히 그에 맞게 식을 조정한다). 위의 평균 시험점수를 구할 때 과목마다 다음과 같은 반영 비율을 준다고 하자.

국어	수학	영어
25%	40%	35%

그러면 평균 시험점수 계산식이 다음과 같이 바뀐다.

 

여기까지가 기본 개념이다. PSAT(또는 여타 적성시험) 자료해석 영역에서 가중평균이 필요한 상황은 보통 어떤 전체 집단의 평균을 내기 위해 하위 집단(보통 2개)의 평균을 이용하는 경우다. 밑에서 실제 문제를 보여주겠지만 예를 들자면,

 

-남성 평균값과 여성 평균값을 이용해 전체 평균값 구하기

-연령대별 평균값을 이용해 (제시된 연령대의) 전체 평균값 구하기

-'전체 평균값과 여성 평균값을 주고 남성 평균값 구하기' 형태로 제시될 수 있음

 

위와 같은 케이스에서는 남성과 여성의 인구 차이, 연령대별 인구 차이 등이 모두 '가중치'로 작용하기 때문에 단순히 산술평균을 이용하다가는 오류가 생길 수 있다.

 

그런데 가중평균을 활용하는 문제가 나왔을 때 위와 같이 식을 일일이 세워서 풀고 있을 수는 없다. 문제에서 가중평균을 활용하려면 기본 개념을 넘어서는 이해가 필요하다.

---

잠시 상상의 나래를 펼쳐 보자. 커다란 줄자 위에서 A, B 두 팀이 줄다리기를 한다. 이 줄자에는 특별한 기능(?)이 있어서, 줄자 위에 선 모든 사람이 각각 똑같은 힘을 낸다. 그런데 A팀은 2명, B팀은 4명이다. A팀은 줄자의 '0' 눈금에서, B팀은 줄자의 '10' 눈금에서 줄을 당기기 시작한다. 이 줄(정확히는 기준이 되는 저 빨간 띠)은 어디에서 멈출까?

 

각자가 내는 힘이 서로 같고 A팀과 B팀의 인원 수가 1:2이므로, A팀이 내는 힘과 B팀의 내는 힘을 비로 표현해도 1:2다. 그렇다면 줄이 멈추는 지점도 두 팀 사이를 1:2로 나눈 어딘가가 될 것이다.

 

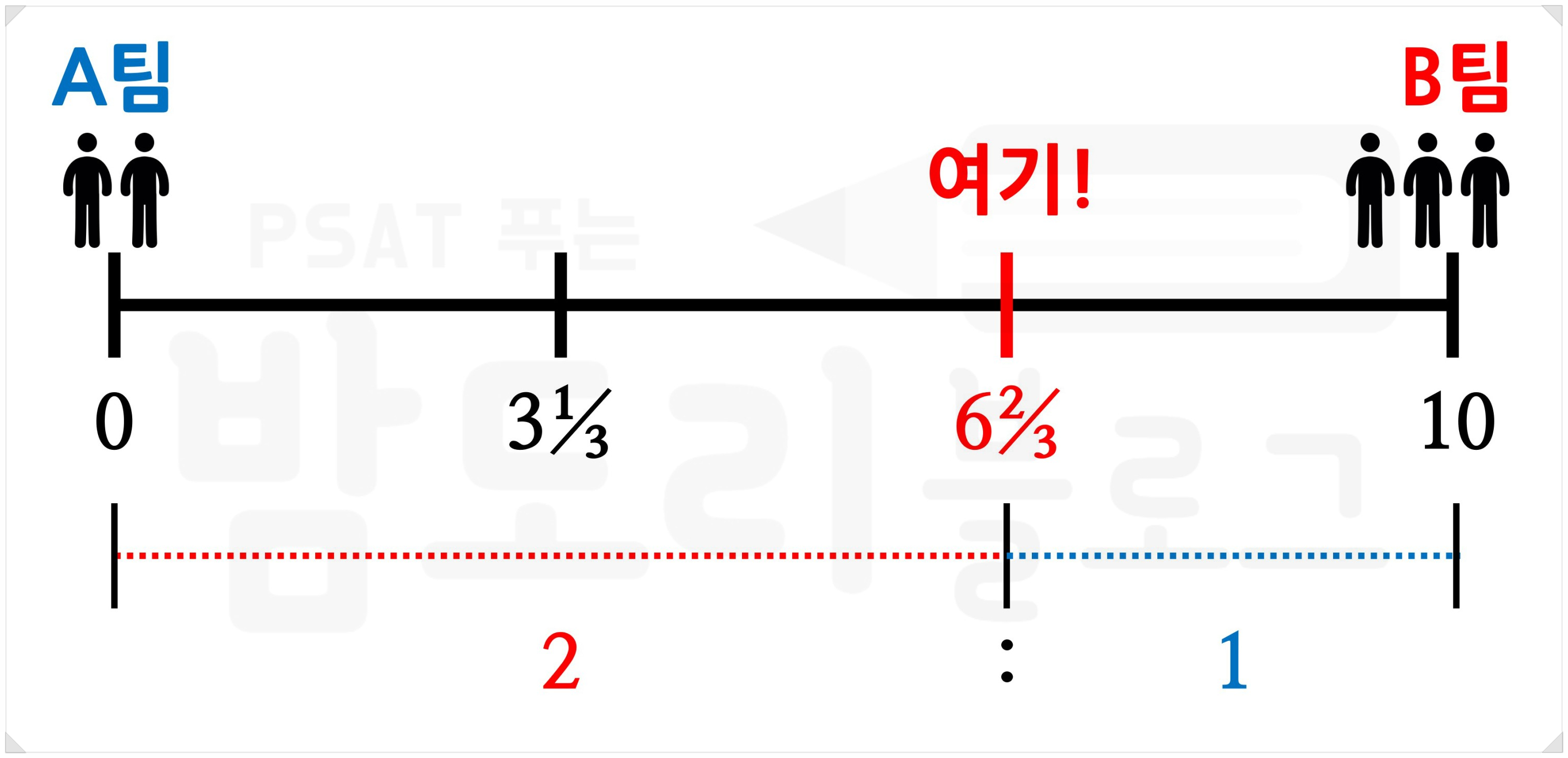
결과부터 이야기하자면 줄은 6⅔ 지점에서 멈춘다. 10을 2:1로 갈라놓은 지점이다. 어라? 아까는 1:2였는데 왜 지금은 2:1이냐고? 힘이 센 쪽으로 줄이 끌려가야 하니까. B팀이 A팀보다 힘이 두 배 센데 줄이 A팀 쪽에 가깝게 멈추면 이상하잖아.

 

그러니 이 줄다리기 그림상에서는 두 팀의 인원(가중치) 비인 1:2가 줄이 멈추는 지점을 계산할 때에는 2:1로 뒤집어지는 것이다. 만약 인원 비가 2:1이라면 줄은 1:2로 나눠지는 3⅓ 지점에서 멈춘다.

 

다른 예시를 한 번 들어보자. 응용수리 단골 소재인 소금물이다. 농도 12%인 소금물 500g과 농도 8%인 소금물 300g을 섞는다. 이 소금물의 농도는 어떻게 될까?

 

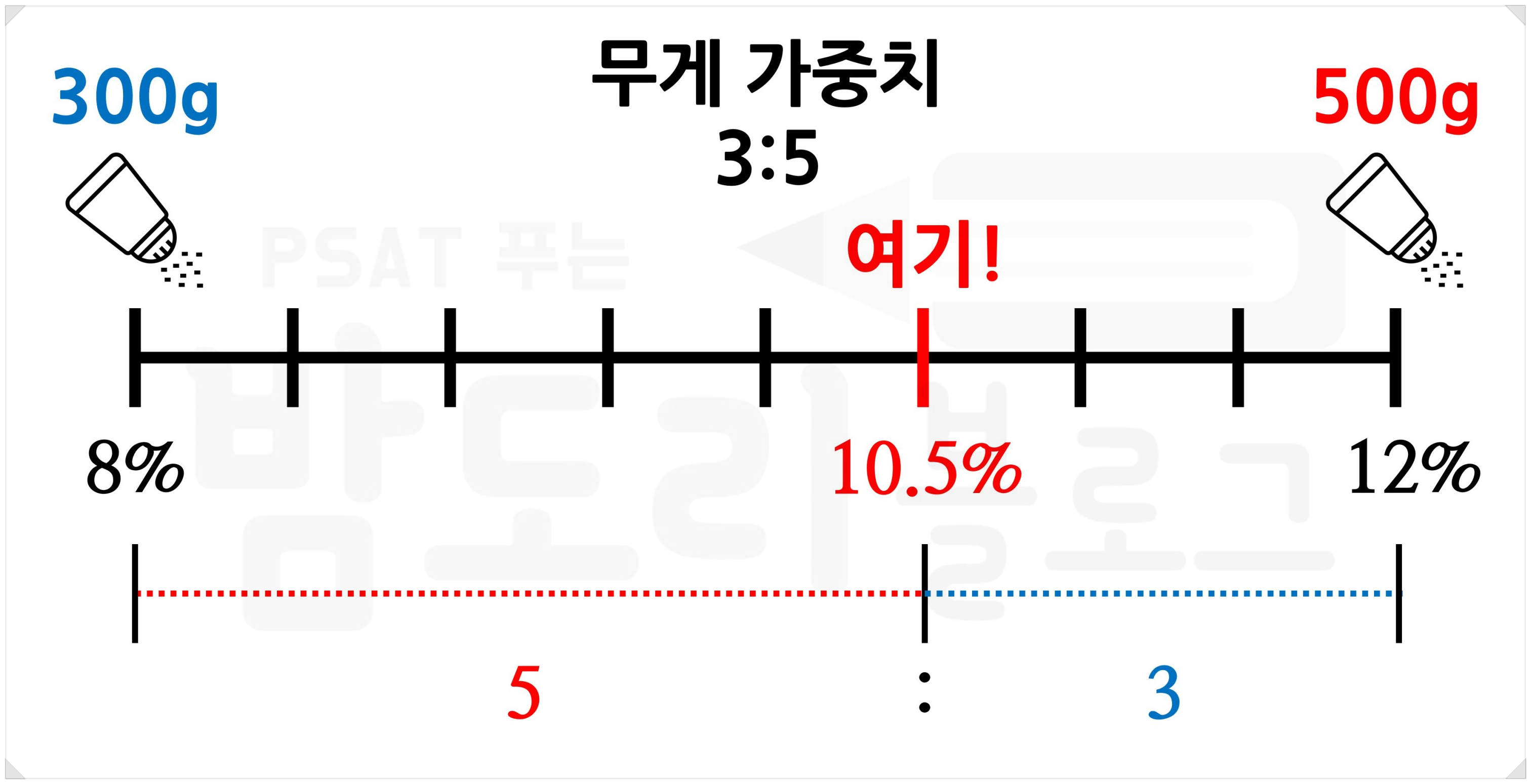
위와 같은 과정을 거쳐 농도 10.5%인 소금물 800g이 될 것이다. 이때 가중치는 소금물 무게에 따라 결정된다. 앞서 든 예시에서는 눈금이 0부터 10까지라 가중치를 적용하기 쉬웠지만 이번에는 눈금이 8%부터 12%까지다. 어떻게 적용된 건지 보이는가? 보인다면 이해한 것이다. 8%부터 12%까지의 거리 4를 5:3 비로 나눠줬다.

 

그러나 문제 풀 때 이렇게 그림을 그리고 있을 수도 없다. 이 과정을 좀 단순화할 수 없을까? 물론 있다.

---

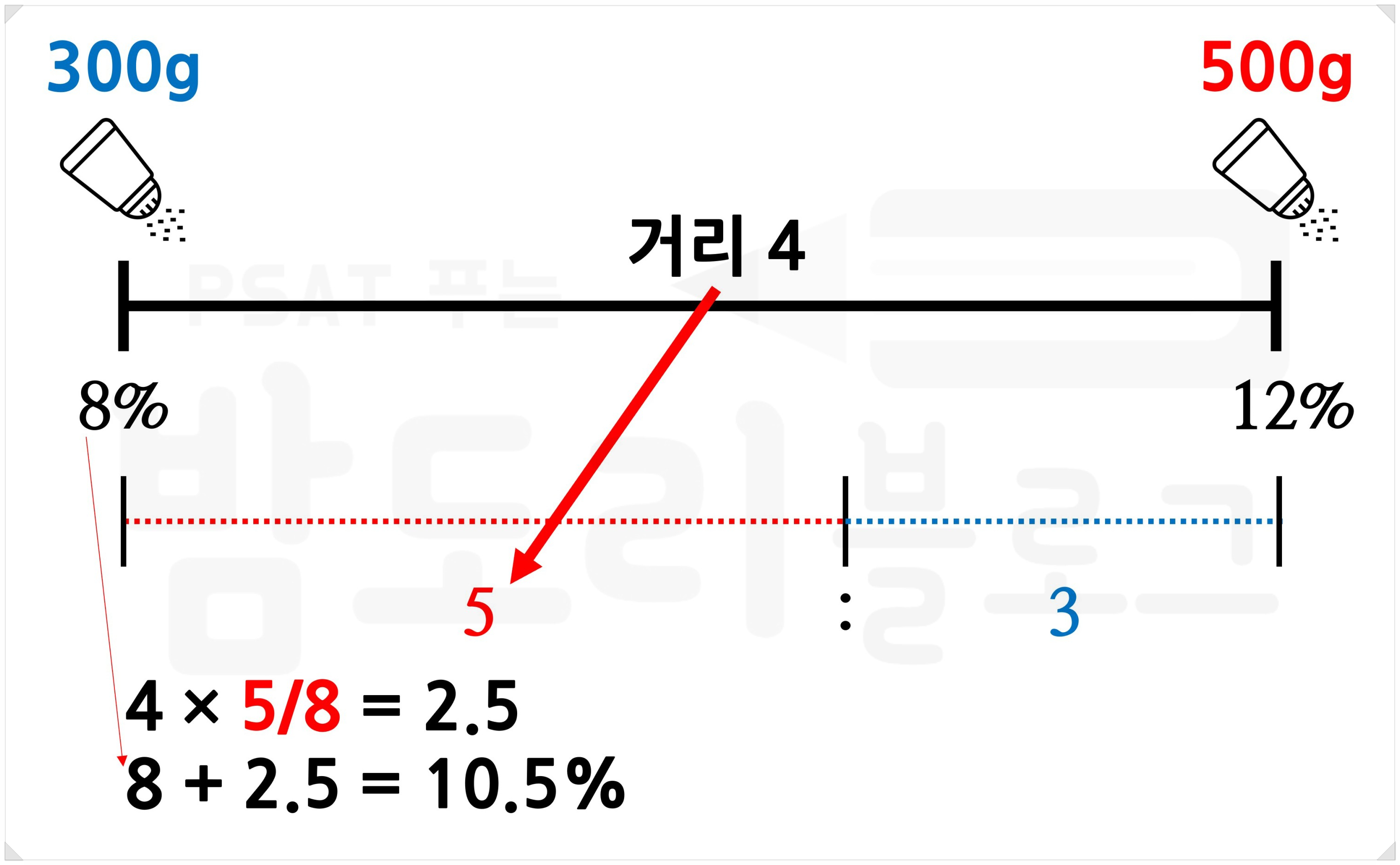
먼저 가중평균을 구하려는 양쪽의 관찰값 차를 구한다. 여기서는 두 소금물의 농도 차에 해당한다. 8%과 12%니까 차는 4.

 

거기에 관찰값이 더 큰 쪽의 가중치를 곱해준다. 두 소금물 중 관찰값이 더 큰 쪽(12%)의 가중치는 5/8이다. 4×5/8=2.5가 나온다. 왜 관찰값이 더 큰 쪽을 이용하냐고? 그게 우리 사고방식상 편하기 때문이다. 더하기는 편하고 빼기는 불편하다. 작은 쪽(8%)에서 큰 쪽(12%)으로 당겨온다고 생각해보자.

 

이 2.5를 더 작은 관찰값인 8%에 더해주면 그게 가중평균값이다. 다른 예시를 들어 보자.

Q. 어떤 설문조사에서 '그렇다'라고 응답한 비율이 남성은 52%, 여성은 61%였다. 설문조사에 응답한 남성은 600명이고 여성은 900명이다. 전체 응답자 중 '그렇다'라고 응답한 비율은?

1) 양쪽의 관찰값 차 구하기

52%와 61%의 차. 9%다.

 

2) 관찰값이 더 큰 쪽의 가중치 구하기

남성 600명, 여성 900명이므로 가중치 비가 2:3이고, 관찰값이 더 큰 여성의 가중치는 3/5이다.

 

3) 1)과 2) 곱하기

9 × 3/5 = 5.4

 

4) 작은 수에 3) 더하기

52% + 5.4 = 57.4%

 

이 과정이 체화되면 숫자가 예쁘게 설계된 문제의 경우 손필기를 거의 하지 않고도 풀 수 있게 된다.

---

지금까지 설명한 건 전부 양쪽의 평균과 가중치가 주어졌을 때 가중평균값을 구하는 방법이다. 그러나 실제로는 반대 방향으로 계산해야 할 때가 더 많다. 가중평균값이 주어져 있고 가중치를 구해야 하는 경우. 기출문제와 함께 보자.

 

문제 속 가중평균 활용: 가중평균값을 이용해 가중치 구하기

2018년 민경채 PSAT 자료해석 가책형 24번

'가중평균 좀 할 줄 아는가?'라고 대놓고 써 있는 문제다. 정말 가중평균만 시킨다. 연합 팀의 인원수와 평균점수를 이용해서 각 팀의 인원수를 구하라고 한다.

 

A+B팀 쪽만 먼저 보자. A팀과 B팀의 인원수가 가중치에 해당하는데 그걸 모른다. 대신 각 팀의 평균점수와 연합팀 평균점수(가중평균값), 연합팀 인원수를 알려줬다. 어떻게 구할 수 있을까? 앞서 소금물 문제 풀 때의 과정을 다시 불러와 보자.

 

1) 양쪽의 관찰값 차 구하기

A팀은 40점, B팀은 60점이므로 차는 20이다.

 

2) 관찰값이 더 큰 쪽의 가중치 구하기

이걸 모른다.

 

3) 1)과 2) 곱하기

4) 작은 수에 3) 더하기

2)는 일단 모르고, 3)과 4)를 거쳐 나온 값이 52.5라는 건 우리가 알고 있다. A팀 40점에 12.5점이 더해졌다는 뜻이다. 우리는 2)에서 '관찰값이 더 큰 쪽의 가중치'를 이용하기로 했으므로, 여기서 나오는 방정식을 풀면 B팀의 가중치를 구할 수 있다.

 

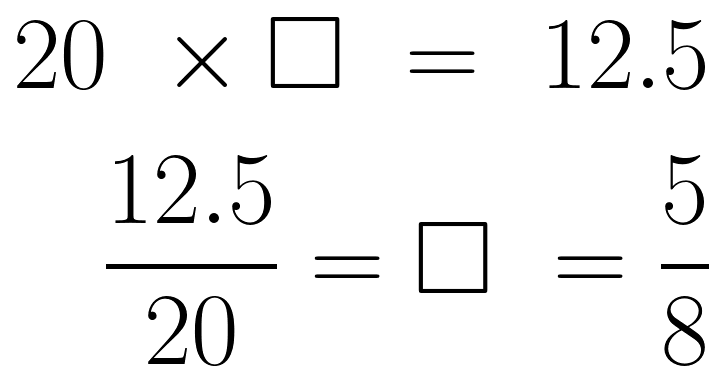
이제 가중치 비가 5:3이라는 걸 알게 되었다. 이건 뒤집힌 거니까 3:5로 바꿔주면 그게 A팀 인원수:B팀 인원수다. 둘이 합쳐 80명이라고 했으니 30명 대 50명으로 깔끔하게 떨어진다.

 

여기서 포인트. 수식에 있는 12.5/20이 B팀의 가중치인데 이게 깔끔하게 약분되지 않는 경우가 있다. 바로 다음 B+C팀을 보자.

 

두 팀의 점수 차가 30점인데 가중평균값은 77.5점이다. 여기서 작은 쪽인 60점을 빼면 17.5점이 남는다. 17.5/30이 C팀 가중치, 나머지인 12.5/30이 B팀 가중치다. 그런데 17.5/30은 자연수로 깔끔하게 약분되지가 않는다. 이럴 때에는 이 가중치를 더는 건드리지 말고 그냥 들고 가자. 우리가 구하려는 건 가중치가 아니라 인원수다.

 

B팀과 C팀을 합쳐 120명이라고 한다. 120명에 위에서 뽑아놓은 가중치를 적용하는 건 쉽다. 분모 30을 120으로 바꿔주면 그만이다. 각각 70/120과 50/120으로 바뀐다. B팀 50명, C팀 70명.

 

좀 더 어려운 예시도 보자.

 

2020년 5급 PSAT 자료해석 나책형 38번

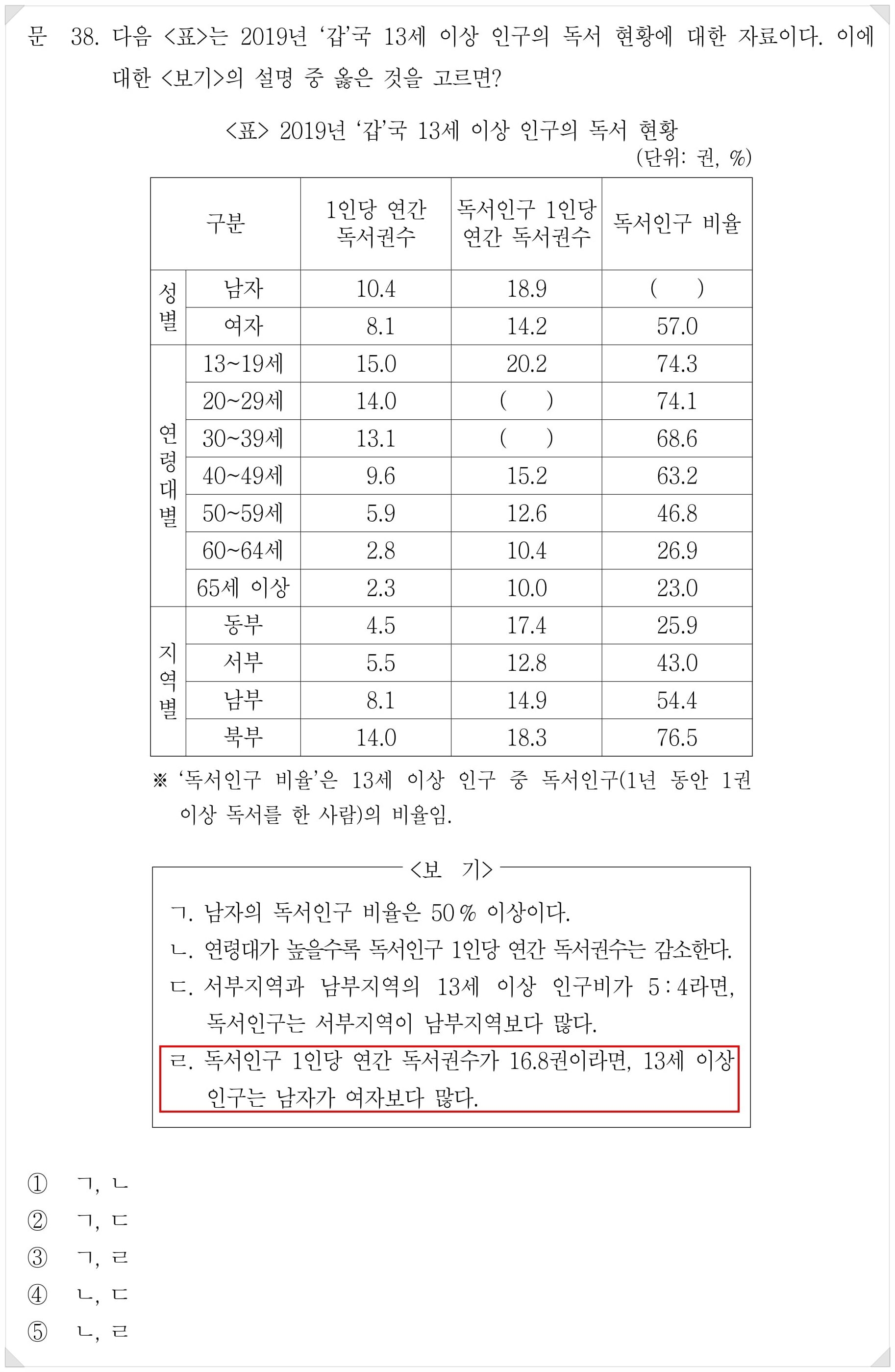
보기 ㄹ만 보자. '독서인구 1인당 연간 독서권수'를 16.8권으로 제시해줬다. 이게 남자(18.9)+여자(14.2)의 가중평균값이다. 이때 독서인구 성비, 즉 가중치를 어떻게 구할 수 있을까? 마지막 단계니까 최대한 압축해보자.

이렇게 표현할 수 있겠다. <표>의 숫자를 대입하면

이렇게 남성 독서인구와 여성 독서인구의 비가 2.6:2.1이라는 걸 알아낼 수 있다. 2.6/4.7과 2.1/4.7은 전체 독서인구 중 각 성별이 차지하는 비율을 의미한다.

 

식으로 양쪽을 다 표현해야 하니 절댓값으로 넣어놓기는 했는데, 실제로는 그냥 '가중평균값-작은 관찰값' 쪽을 먼저 계산한 뒤 나머지 부분을 반대편 가중치로 삼으면 된다. 남성 독서인구 가중치인 2.6/4.7을 구했으면 (1을 기준으로) 나머지인 2.1/4.7이 자연스레 여성 독서인구 가중치가 된다는 뜻이다.

---

앞서 소개한 방법들을 이용해 풀 수 있는 가중평균 연습문제다.

가중평균 연습문제.pdf

0.10MB

값이 정확히 안 떨어지면 대충 근삿값을 적으면 된다(그러라고 만든 숫자다).

가중평균 연습문제_정답.pdf

0.06MB

어느 쪽 가중치가 큰지만 확인하기

지금까지는 가중치를 모두 정확히 구했지만 실제로는 어느 쪽 가중치가 더 큰지만 확인해도 문제를 풀 수 있는 경우가 있다. 방법은 간단한다. 주어진 가중평균값과 양쪽 관찰값의 차를 비교하는 것이다. 가중평균값과 더 가까운 쪽의 가중치가 더 크다.

 

2016년 입법고시 PSAT 자료해석 가책형 24번

위 문제 1번 선지만 보자. 중고령층 단순노무 종사자 중 남성이 많은지 여성이 많은지를 묻고 있다. <표>에는 전체(가중평균값)와 남녀 각각의 관찰값이 모두 주어져 있으므로, 앞서 본 방법대로 남녀 각각의 가중치를 정확히 구할 수는 있다. 그러나 그렇게까지 푸는 건 낭비다. 이 선지에서 알아야 할 건 '남성이 여성보다 많은가?'뿐이기 때문이다.

 

줄다리기 비유로 돌아가 보자. A팀 인원이 B팀보다 많으면 당연히 줄은 A팀 쪽으로 끌려가 멈춘다. 이때 줄이 멈춘 곳은 B팀보다 A팀에 가까울 것이다. 같은 원리를 역으로 적용하면, 가중평균값과의 관찰값 차가 더 적은 쪽의 가중치가 더 크다.

 

다시 문제로 돌아가서… '중고령층 단순노무 종사자' 전체의 주당평균근로시간은 42.6시간이다. 이게 가중평균값이다. 그리고 남성 평균은 45.7, 여성 평균은 38.8. 어느 쪽이 가중평균값에 더 가까운가? 남성 평균과는 3.1 차이가 나고 여성 평균과는 딱 봐도 3.1보다는 큰 차이가 난다. 여기까지만 보고 남성이 여성보다 많다는 결론을 낼 수 있다.

 

+) 위 문제는 통째로 가중평균 활용 문제이므로 글의 내용을 모두 이해했다면 2, 3, 5번 선지를 풀어보자.

 

삼중 가중평균

인사혁신처가 출제하는 PSAT에서는 삼중 가중평균이 거의 나오지 않는다. 그러나 아주 가아끔 출제되었는데… 이 경우에는 삼중 가중평균을 한 번에 풀 것을 요구하지는 않는다(그럼 시간을 너무 잡아먹어서 노양심이다). 이중 가중평균을 두 번 해서 풀 수 있거나 굳이 가중평균값을 구하지 않아도 답을 알 수 있도록 설계한다. 악명높은 2016년 기출을 보자.

 

2016년 5급 PSAT 자료해석 4책형 18번

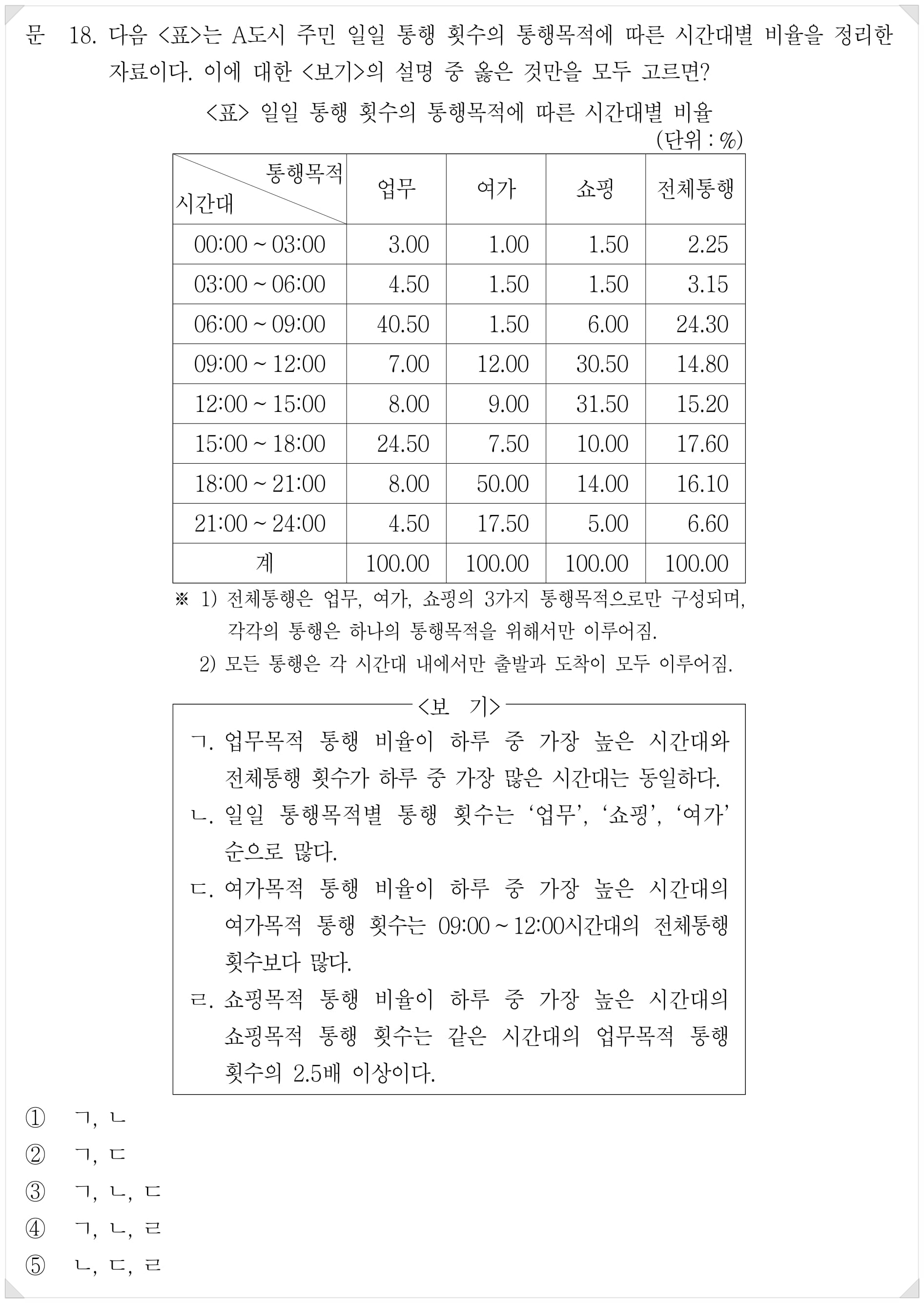
이 문제는 업무, 여가, 쇼핑 각각의 가중치를 알아야 풀 수 있다. 그런데 잘 보면 셋 중 두 항목의 관찰값(통행 횟수 비율)이 같은 시간대가 있다. 3시~6시에 여가와 쇼핑이 같다. 이러면 업무와 여가+쇼핑으로 묶어 위에서 해왔던 것처럼 가중평균을 편하게 할 수 있게 된다.

 

가중평균값이 3.15이고 작은 쪽이 1.50이므로

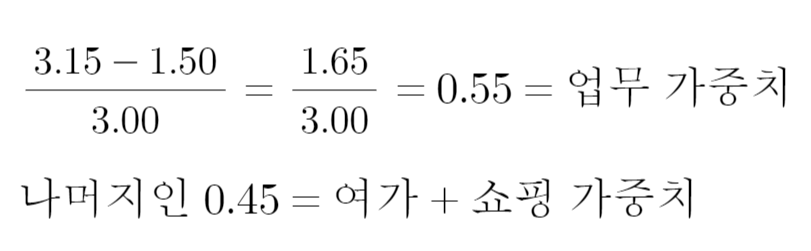
이제 여가와 쇼핑만 나눠주면 되는데 이때는 숫자가 좀 보기 좋게 생긴 0시~3시 시간대를 이용한다. 업무 항목을 빼야 하므로 전체 가중평균값 2.25에서 업무 3.00×0.55=1.65를 빼준다.

 

남은 0.6을 가지고 여가와 쇼핑의 가중치를 구해보자. 이때 주의할 점. 업무가 빠졌으므로 가중치의 합이 0.45인 상태다. 우리는 가중치의 합이 1이라는 가정하에 계산을 해왔으므로, 그 방식을 고대로 사용하려면 여가와 쇼핑 각각의 관찰값에 0.45를 곱해줘야 한다. 계산할 때 필요한 건 관찰값이 작은 여가뿐이므로 크게 귀찮은 작업은 아니다.

이걸 보여주긴 해야 할 것 같아서 적었지만 실제로는 최고난이도 문항이라 넘기는 게 득이다. 합격권 점수 확보를 위해 이렇게까지 마스터할 필요는 없을 것이다. 다만 이중 가중평균은 확실하게 체화하는 게 좋다.

 

끝

가중평균을 어떻게 활용하는지 똑같이 아는 사람끼리도, 분수-소수 변환 감각에 따라 퍼포먼스 차이가 날 수 있다. 위에서 보여줬던 ABC팀 문제에서는 12.5/20를 보고 바로 n/8 단위를 떠올릴 수 있느냐에 따라 시간을 얼마나 쓸지가 결정된다(1/8=0.125를 달달 외우거나 아예 체화한 사람이라면 안 떠오를 수가 없다). 주요 계산값들을 외우거나 체화하는 건 정말 다방면으로 활용 가능하니 웬만하면 빼먹지 말자. 분모가 한 자릿수인 분수들은 던졌을 때 바로바로 튀어나올 수준이면 좋다.

 

시리즈마냥 계속 쓰게 된다면 다음 글에서는 변화율 역산을 다룰 예정이다.

밤도리 프리미엄콘텐츠: 가중평균 훈련자료

가중평균을 위한 암산 훈련