for PSAT 자료해석: 변화율(증가율)·비중 역산

사실 못 풀지는 않는데 오래 걸린다

가중평균에 이은 두 번째 글이다. 변화율(증가율)·비중 역산은 가중평균보다도 더 많이 써먹어야 하는 개념이다. 요구되는 사고의 난이도는 낮지만 은근히 이걸 못하거나 속도가 안 나오는 경우가 많다. 내가 사용하는 방법을 중심으로 정리해보았다.

 

<다른 'for PSAT 자료해석' 글>

for PSAT 자료해석: 가중평균 이론과 활용

비율 변화율 역산 훈련

변화율(증가율) 역산

PSAT 자료해석에서 사용되는 변화율은 보통 증가율이다. 편의상 증가율을 이용해 설명하겠다(감소율도 원리는 같으므로 따로 설명할 필요가 없다). 이 글에서 말하는 '변화율 역산'이란 변화율이 주어졌을 때 초기값(변화하기 전의 값)을 구하는 것을 말한다. 계산을 역으로 하려면 정방향으로 하는 법부터 살펴야겠지? 초기값에 변화율을 적용하는 식부터 정리해보자.

 

위의 식은 백분율(%)을 기준으로 한 것이고, 아래의 식은 %를 제거했을 때의 식이다

 

예를 들어 2021년 A회사 평균연봉이 5000만 원이고, 이게 2022년에 5% 인상된다고 하면 다음과 같은 식이 도출된다(다른 변수는 없다고 가정하자).

 

당연한 얘기지만 실제로 이걸 이렇게까지 써가며 계산할 일은 없고 5000에 5% 증가한다고 하면 바로 250을 더하는 암산이 튀어나와야 정상이다. 이 정방향의 계산은 특별히 설명할 게 없다(다 알 거고). 문제는 역산이다.

 

Q. 연봉이 전년대비 5% 오른 A사원의 2021년 연봉은 8400만 원이다. A사원의 2020년 연봉은?

 

이렇게 후기값과 증가율만 주고 초기값을 구해야 하는 상황이 자주 주어진다. 이 문제를 풀기 위한 식을 쓴다면 다음과 같을 것이다.

 

 

왜 105로 나누고 100을 곱하는지 이해되는가? 백분율에서 기준값은 100%이고, 변화율 계산 상황에서는 초기값이 100%에 해당한다. 그럼 초기값에 5%를 더한 후기값은 105%일 것이다. 이걸 다시 100%(초기값)으로 되돌려주려면 105로 나누고 100을 곱하면 된다.

 

그런데 모든 변화율 역산을 이렇게 일일이 식 써가며 풀 수는 없다. 지금은 숫자들이 8400, 5%로 아주 예뻐서 그렇지 실제 PSAT 자료해석 문제에서 이렇게 깔끔한 숫자만 주는 경우는… 거의 없다. 이 원리를 바탕으로 다른 방법을 쓸 수 있어야 한다.

 

앞서는 증가율이 5%였지만 이번에는 증가율이 50%인 경우를 생각해보자. 후기값과 함께 증가율 50%가 주어졌다면 초기값을 어떻게 구할 수 있을까? 후기값이 150%니까 150으로 나누고 100을 곱하면… 음? 약분되지 않나?

 

그렇다. 이렇게 간단한 분수식으로 바뀌는 경우가 굉장히 많다. 이 원리를 좀 더 풀면 다음과 같다.

 

증가율이 50%라면 초기값의 절반, 즉 1/2만큼 증가했다는 뜻이다. 그럼 후기값은 초기값의 3/2가 된다. 이를 다시 초기값으로 되돌리려면 역(2/3)을 곱하면 되는 것이다. 만약 증가량만 똑 떼고 싶다면 1/3을 곱하면 되고. 이 원리는 분수로 만드는 게 편한 수많은 경우에 활용할 수 있다.

 

증가량이 1/n인 경우들. 이미지의 증가량은 초기값 기준이다.

초기값이 아니라 변화량(증가량)을 구해야 한다면 후기값의 역에서 분자만 1로 바꿔주면 된다. 예를 들어 증가율이 33%라면 증가량은 후기값 × 1/4이다. 위와 같이 자주 써먹을 수 있는 증가율-분수 변환값들을 소개한다.

 

한편 증가율이 꼭 저런 예시들에 딱 들어맞아야만 하는 건 아니다. PSAT 자료해석 영역 특성상 저기서 조금 벗어나는 변화율을 대충 퉁쳐도(?) 푸는 데 지장이 없다. 예를 들어 증가율이 34.x% 정도로 주어졌으면 대충 1/3이라고 보고 풀어도 된다. 16%든 17%든 둘 다 1/6로 퉁칠 수 있고.

 

위의 방법은 초기값 또는 변화량을 비교적 정확하게 구할 때 유용하다. 그런데 실제로는 그 값을 정확하게 구하지 않고도 문제를 풀 수 있는 경우가 더 많다. 실례를 보자.

---

2020년 5급 PSAT 자료해석 나책형 11번

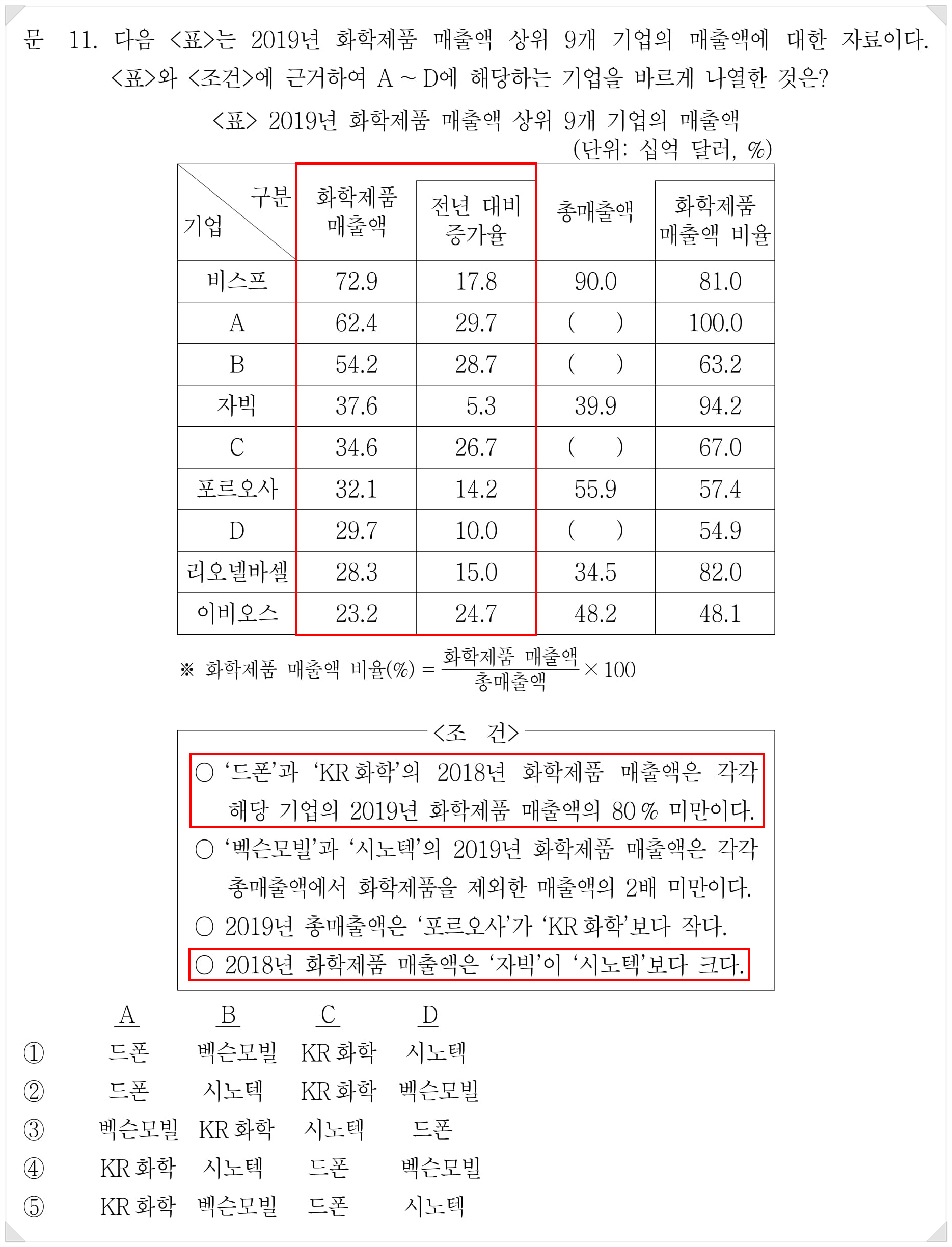
위 문제에서 빨간 네모 칸만 보자. 증가율 부분이다. 이 문제는 각 기업의 2018년(전년) 화학제품 매출액을 정확히 구해야 풀 수 있는 문제가 아니다. 2018년 화학제품 매출액이 걸려 있는 조건1, 조건4만 따져보자.

 

먼저 조건1부터. 이 조건은 초기값(2018년 화학제품 매출액)이 후기값(2019년 화학제품 매출액)의 80% 미만인지를 묻고 있다. <표>에 주어진 건 증가율과 후기값이다. 앞서 본 원리를 생각해보자. 80%는 4/5이므로, 후기값에 4/5를 곱해 초기값이 나온다면 증가량은 초기값의 1/4에 해당한다. 그래야 후기값이 5/4가 되고, 역을 곱할 때 4/5를 곱하게 되니까. 말로 하려니까 좀 복잡해지는 것 같은데 정리하면 아래와 같다.

 

만약 증가율이 25%(1/4)보다 작다면 후기값도 5/4보다 작아지고, 초기값은 후기값의 4/5(80%)보다 커진다. 따라서 조건1은 '전년 대비 증가율'이 25%보다 큰 곳을 찾으라는 뜻이다.

 

조건4는 어떨까? 자빅의 초기값이 시노텍보다 크다고 한다. 만약 위의 조건들을 해결해두었다면 조건4를 풀 때는 B와 D 정도만 비교하게 된다. 초기값을 일일이 구해봐야 할까? 그렇지 않다. 자빅의 초기값부터 생각해보자. 5.3% 증가해서 37.6이 되었다. 정석대로 식을 쓴다면 37.6 ÷ 105.3 × 100이 되겠지만 누가 미쳤다고 시험 시간에 이걸 쓰고 있을까?

 

이때는 37.6에서 정직하게 5%쯤을 빼주는 게 효율적이다. 그래서 자빅의 2018년 화학제품 매출액을 대충 35~36 사이로 잡는다. 물론 이렇게 계산하면 정확한 값이 나오지 않는다. 그러나 문제 푸는 데 지장이 생길 만큼의 오차도 나오지 않는다. 10% 이내의 변화율은 이렇게 처리해도 큰 오차가 없다.

 

변화율을 그대로 빼 버리면 위와 같이 오차가 발생하지만, 변화율이 작을수록 오차도 작다.

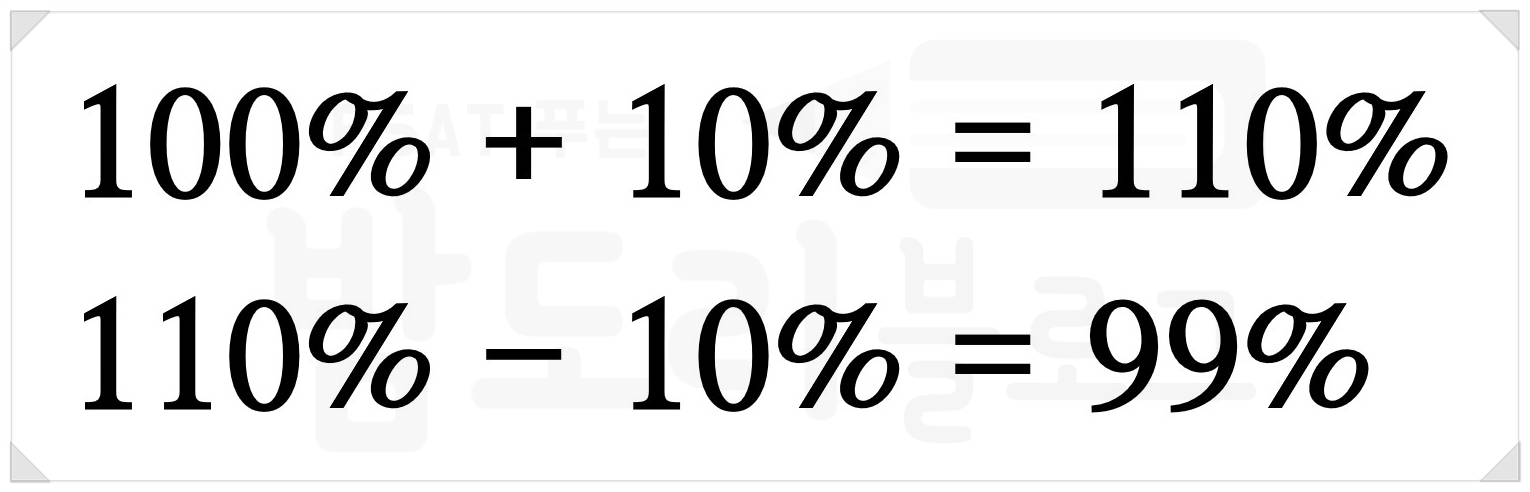
그러고 나서 B, D를 보면… D는 10% 증가해서 고작 29.7이 되었다. 증가하기 전에는 당연히 이보다 작았다는 이야기이므로 더 볼 것도 없다. D의 2018년 화학제품 매출액은 자빅보다 작다. 그럼 B는?

 

28.7% 증가해서 54.2가 되었다. 어떻게 검증할까? 위에서 소개한 방법대로 한다면 28.7%를 대충 2/7이라고 생각하고 54.2에 7/9을 곱할 수 있다. 9×6=54니까, 6×7=42 해서 바로 40보다 크다는 걸 알 수 있다. 또 다른 방법도 있다.

 

숫자를 좀 더 단순화해서 가정법을 쓰는 것이다. 앞서 자빅의 2018년 화학제품 매출액을 30대로 뽑아 놓았으니 B의 2018년 화학제품 매출액을 40이라고 생각하고, 전년대비 증가율은 30%로 반올림해준다. 40에서 30% 증가하면 54.2가 될 수 있느냐는 사고다. 물론 40+30%(40의 1.3배)로는 54.2가 안된다. 그런데 실제 증가율은 30%보다도 작으므로 B의 2018년 화학제품 매출액은 40보다 더 커져야 한다.

---

정리하면,

 

1) 초기값은 100%이다.

2) 후기값은 (100+변화율)%이다.

3) 초기값/후기값이나 변화율을 분수로 바꾸면 수월하게 역산할 수 있다.

4) 원리를 활용해서 초기값/후기값/변화율의 범위까지만 구하는 것도 가능

 

변화율 역산은 이제부터 설명할 비중 역산과 어느 정도 상호작용하는 측면이 있다. 두 개념을 모두 이해하면 어느 쪽이든 매우 수월해진다.

 

비중 역산

비중 계산도 변화율만큼이나 자주, 아니 오히려 더 많이 쓰인다. 다 아는 내용이겠지만 비중의 개념부터 되짚고 가자. 가장 자주 사용되는 'A 대비 B 비중'의 경우 다음과 같이 수식화된다.

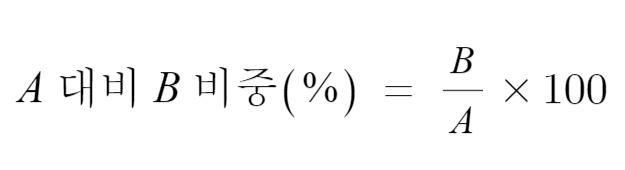
%를 붙이지 않는 경우 뒤에서 ×100을 빼고, 기준을 1로 삼아 표기한다.

 

식이 이렇게 간단하니 계산 방향도 간단하게 두 가지 나온다. A와 비중을 주고 B를 구하게 만들거나, B와 비중을 주고 A를 구하게 하거나. 정방향 계산인 전자는 매우 간단하다. 예를 들어 전체 과일 수확량 1200개 중 사과 수확량 비율이 35%라고 하자.

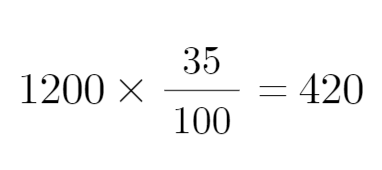
이건 손계산할 것도 없이 암산할 수 있는 간편한 계산이다. 그럼 역산은 뭔가? 사과 수확량 420개를 주고, 이게 전체 과일 수확량의 35%라면 전체 과일 수확량은 몇 개인가를 묻는다. 이때는 식으로 표현하면 이렇다.

계산을 역으로 하니 아까처럼 편한 곱셈식이 나오지 않는다. 35로 나누고 100을 곱해줘야 한다. 그런데 변화율 역산도 그랬지만 비중 역산을 이렇게 일일이 식 써가며 할 수는 없다. 변화율 역산처럼 좀 더 단순한 사고가 필요하다.

 

A 대비 B에서 기준은 A다. 백분율로 표기할 경우 A는 기준값인 100%에 해당한다. 즉, 비중 역산은 100%가 안되는 B의 값을 100%로 만드는 과정과 같다. 뭐로 나누고 100을 곱하는 게 아니라 처음부터 B 비중에 몇을 곱해서 100%를 만든다고 생각하자.

 

이런 식이다

이게 결국은 역을 곱하는 식에서 분수를 소수로 바꿔놓은 것과 같지 않냐! 고 할 수 있는데, 처음부터 곱셈으로 접근하는 것과 나눗셈을 거쳐가는 건 요구되는 사고의 양이 다르다. 처음부터 '몇을 곱하면 100이 되는가'를 생각하는 쪽이 훨씬 편하다. 애당초 나눗셈을 암산할 때도 이 방식을 사용한다.

 

위에 쓴 예시들은 매우 예쁜 숫자들이라 정확한 값이 술술 나오겠지만 실제로는 못생긴(…) 비중을 줄 수도 있다. PSAT 자료해석은 계산이 매우 정확할 필요가 없는 시험이므로 곱해서 100 만들기를 '대충' 적용하면 된다.

 

아, 경우에 따라서는 곱해서 100을 만드는 게 아니라 나눠서 10이나 1을 만드는 게 더 편할 수도 있다. 자릿수 변환은 0만 붙이면 되는 거니까. 예를 들어 비중 20%짜리를 줬을 때 곱하기 5보다 나누기 2가 편할 수 있다는 것이다. 곱하기 5가 편하냐 나누기 2가 편하냐는 숫자마다 다르기 때문에 경험을 쌓다 보면 자신만의 감이 만들어지리라 본다.

 

기출문제를 보자.

---

2021년 7급 PSAT 자료해석 나책형 8번

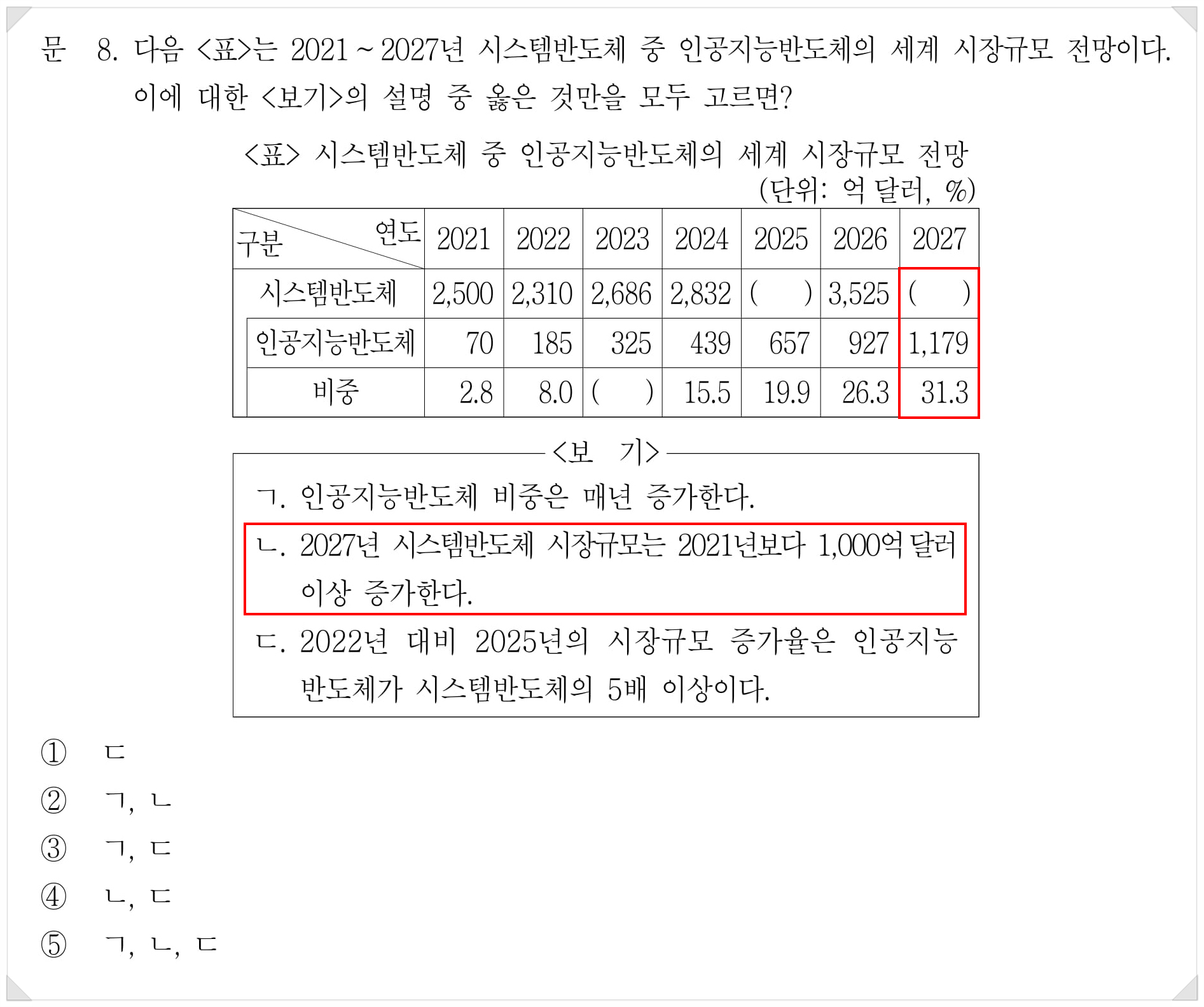
보기 ㄴ이다. 비중 역산의 전형이다. 2021년 시스템반도체 시장규모는 2500으로 나와 있고 2027년에 그게 3500 이상인지를 따져야 한다. 인공지능반도체와 그 비중이 나와 있으니 식을 쓴다면 다음과 같을 것이다.

 

여러 번 말했듯 식 써서 푸는 건 최악이다. 소개한 방법대로 31.3에 몇을 곱해야 100이 되는지 생각해보자. 단, 정확히 말고 대충.

 

일단 곱하기 3까지는 들어갈 것 같다. 31.3에 곱하기 3 하면 93.9다. 남은 6.1을 채워줘야 하는데… 아니, 채우기 전에 확인할 게 있다. 우리가 구하려는 건 2027년 시스템반도체 시장규모의 정확한 값이 아니다. 2027년 시스템반도체 시장규모가 3500 이상인지 아닌지만 알면 된다. 최소한 곱하기 3이 들어가야 하는 건 확인했으니 1179에 3을 곱해보자. 3500을 넘는다. 여기까지다.

※ 1179×3은 1000×3과 170×3으로 분리된다. 일의 자리 9는 일단 무시.

 

변화율 역산할 때 본 기출문제에도 비중 파트가 있다.

 

2020년 5급 PSAT 자료해석 나책형 11번

딱 하나만 짚으려고 가져왔다. C의 화학제품 매출액 비율이 67%다. 이걸 보면 바로 3분의 2가 떠올라야 한다. 그럼 1.5를 곱해서 100%가 되는 게 바로 보이기 때문이다. 마침 C의 화학제품 매출액 34.6도 1.5 곱하기 좋게(?) 생겨먹었다.

끝

굉장히 어려운 이론이 아니라서 익히는 데 오래 걸리지는 않을 거고, 얼마나 체화하느냐가 관건이다. 자주 나오는 분수나 소수, 백분율끼리의 환산이 빠르면 매우 유리하기 때문에 1/2~1/9 정도의 변환값은 외우면 편하다.

밤도리 프리미엄콘텐츠: 역산 훈련자료

비율 변화율 역산 훈련